Confidential Assets

Table of Contents

• Introduction
• Preliminaries
• Basis of Confidential Assets
  • Confidential Transactions
  • Asset Commitments and Surjection Proofs
  • Confidential Asset Scheme
    • Asset Transactions
    • Asset Issuance
    • Asset Reissuance
    • Flexibility
• Confidential Asset Implementations
  • Elements Project
  • Chain Core Confidential Assets
  • Cloak
• Conclusions, Observations and Recommendations
• References
• Appendices
  • Appendix A: Definition of Terms
  • Appendix B: Ricardian Contracts vs. Smart Contracts
• Contributors

Introduction

Confidential assets, in the context of blockchain technology and blockchain-based cryptocurrencies, can have different meanings to different audiences, and can also be something totally different or unique depending on the use case. They are a special type of digital asset and inherit all its properties, except that they are also confidential. Confidential assets therefore have value, can be owned but have no physical presence. The confidentiality aspect implies that the amount of assets owned, as well as the asset type that was transacted in, can be confidential. A further classification can be made with regard to whether they are fungible (interchangeable) or non-fungible (unique, not interchangeable). Confidential assets can only exist in the form of a cryptographic token or derivative thereof that is also cryptographically secure, at least under the Discrete Logarithmic Problem^def (DLP) assumption.

The basis of confidential assets is confidential transactions as proposed by Maxwell [4] and Poelstra et al. [5], where the amounts transferred are kept visible only to participants in the transaction (and those they designate). Confidential transactions succeed in making the transaction amounts private, while still preserving the ability of the public blockchain network to verify that the ledger entries and Unspent Transaction Output (UTXO) set still add up. All amounts in the UTXO set are blinded, while preserving public verifiability. Poelstra et al. [5] showed how the asset types can also be blinded in conjunction with the output amounts. Multiple asset types can be accommodated within single transactions on the same blockchain.

This report investigates confidential assets as a natural progression of confidential transactions.

Preliminaries

This section gives the general notation of mathematical expressions when specifically referenced in the report. This notation is important pre-knowledge for the remainder of the report.

• Let $ p ​$ be a large prime number.
• Let $ \mathbb G $ denote a cyclic group of prime order $ p $.
• Let $ \mathbb Z_p $ denote the ring of integers $ modulo \mspace{4mu} p $.
• Let $ \mathbb F_p $ be a group of elliptic curve points over a finite (prime) field.
• All references to Pedersen Commitment will imply Elliptic Curve Pedersen Commitment.

Basis of Confidential Assets

Confidential transactions, asset commitments and Asset Surjection Proofs (ASPs) are really the basis of confidential assets. These concepts are discussed in the following sections.

Confidential Transactions

Confidential transactions are made confidential by replacing each explicit UTXO with a homomorphic commitment, such as a Pedersen Commitment, and made robust against overflow and inflation attacks by using efficient zero-knowledge range proofs, such as a Bulletproof [1].

Range proofs provide proof that a secret value, which has been encrypted or committed to, lies in a certain interval. They prevent any numbers coming near the magnitude of a large prime, say $ 2^{256} $, that can cause wraparound when adding a small number, e.g. proof that a number $ x \in [0,2^{64} - 1] $.

Pedersen Commitments are perfectly hiding (an attacker with infinite computing power cannot tell what amount has been committed to) and computationally binding (no efficient algorithm running in a practical amount of time can produce fake commitments, except with small probability). The Elliptic Curve Pedersen Commitment to value $ x \in \mathbb Z_p $ has the following form:

\[C(x,r) = xH + rG \tag{1}\]

where $ r \in \mathbb Z_p $ is a random blinding factor, $ G \in \mathbb F_p $ is a random generator point and $ H \in \mathbb F_p $ is specially chosen so that the value $ x_H $ satisfying $ H = x_H G $ cannot be found, except if the Elliptic Curve DLP^def (ECDLP) is solved. The number $ H $ is what is known as a Nothing Up My Sleeve (NUMS) number. With secp256k1, the value of $ H $ is the SHA256 hash of a simple encoding of the $ x $-coordinate of the generator point $ G $. The Pedersen Commitment scheme is implemented with three algorithms: Setup() to set up the commitment parameters $ G $ and $ H $; Commit() to commit to the message $ x $ using the commitment parameters $ r $, $ H $ and $ G $; and Open() to open and verify the commitment ([5], [6], [7], [8]).

Mimblewimble ([9], [10]) is based on and achieves confidentiality using these confidential transaction primitives. If confidentiality is not sought, inputs may be given as explicit amounts, in which case the homomorphic commitment to the given amount will have a blinding factor $ r = 0 ​$.

Asset Commitments and Surjection Proofs

The different assets need to be identified and transacted with in a confidential manner, and proven to not be inflationary. This is made possible by using asset commitments and ASPs ([1], [14]).

Given some unique asset description $ A $, the associated asset tag $ H_A \in \mathbb G $ is calculated using the Pedersen Commitment function Setup() using $ A $ as auxiliary input. (Selection of $ A $ is discussed in Asset Issuance.) Consider a transaction with two inputs and two outputs involving two distinct asset types $ A $ and $ B $:

\[\begin{aligned} in_A = x_1H_A + r_{A_1}G \mspace{15mu} \mathrm{,} \mspace{15mu} out_A = x_2H_A + r_{A_2}G \\\\ in_B = y_1H_B + r_{B_1}G \mspace{15mu} \mathrm{,} \mspace{15mu} out_B = y_2H_B + r_{B_2}G \end{aligned} \tag{2}\]

In the equations that follow, a commitment to the value of $ 0 $ will be denoted by $ (\mathbf{0}) $, i.e. $C(0,r) = 0H + rG = (\mathbf{0})$. For relation (2) to hold, the sum of the outputs minus the sum of the inputs must be a commitment to the value of $ 0 $:

\[\begin{aligned} (out_A + out_B) - (in_A + in_B) = (\mathbf{0}) \\\\ (x_2H_A + r_{A_2}G) + (y_2H_B + r_{B_2}G) - (x_1H_A + r_{A_1}G) - (y_1H_B + r_{B_1}G) = (\mathbf{0}) \\\\ (r_{A_2} + r_{B_2} - r_{A_1} - r_{B_1})G + (x_2 - x_1)H_A + (y_2 - y_1)H_B = (\mathbf{0}) \end{aligned} \tag{3}\]

Since $ H_A $ and $ H_B $ are both NUMS asset tags, the only way relation (3) can hold is if the total input and output amounts of asset $ A $ are equal and if the same is true for asset $ B $. This concept can be extended to an unlimited amount of distinct asset types, as long as each asset tag can be a unique NUMS generator. The problem with relation (3) is that the asset type of each output is publicly visible, thus the assets that were transacted in are not confidential. This can be solved by replacing each asset tag with a blinded version of itself. The asset commitment to asset tag $ H_A $ (blinded asset tag) is then defined as the point

\[H_{0_A} = H_A + rG \tag{4}\]

Blinding of the asset tag is necessary to make transactions in the asset, i.e. which asset was transacted in, confidential. The blinded asset tag $ H_{0_A} $ will then be used in place of the generator $ H $ in the Pedersen Commitments. Such Pedersen Commitments thus commit to the committed amount as well as to the underlying asset tag. Inspecting the Pedersen Commitment, it is evident that a commitment to the value $ x_1 $ using the blinded asset tag $ H_{0_A} $ is also a commitment to the same value using the asset tag $ H_A $:

\[x_1H_{0_A} + r_{A_1}G = x_1(H_A + rG) + r_{A_1}G = x_1H_A + (r_{A_1} + x_1r)G \tag{5}\]

Using blinded asset tags, the transaction in relation (2) then becomes:

\[\begin{aligned} in_A = x_1H_{0_A} + r_{A_1}G \mspace{15mu} \mathrm{,} \mspace{15mu} out_A = x_2H_{0_A} + r_{A_2}G \\\\ in_B = y_1H_{0_B} + r_{B_1}G \mspace{15mu} \mathrm{,} \mspace{15mu} out_B = y_2H_{0_B} + r_{B_2}G \end{aligned} \tag{6}\]

Correspondingly, the zero sum rule translates to:

\[\begin{aligned} (out_A + out_B) - (in_A + in_B) = (\mathbf{0}) \\\\ (x_2H_{0_A} + r_{A_2}G) + (y_2H_{0_B} + r_{B_2}G) - (x_1H_{0_A} + r_{A_1}G) - (y_1H_{0_B} + r_{B_1}G) = (\mathbf{0}) \\\\ (r_{A_2} + r_{B_2} - r_{A_1} - r_{B_1})G + (x_2 - x_1)H_{0_A} + (y_2 - y_1)H_{0_B} = (\mathbf{0}) \end{aligned} \tag{7}\]

However, using only the sum to zero rule, it is still possible to introduce negative amounts of an asset type. Consider blinded asset tag

\[H_{0_A} = -H_A + rG \tag{8}\]

Any amount of blinded asset tag $ H_{0_A} $ will correspond to a negative amount of asset $ A $, thereby inflating its supply. To solve this problem, an ASP is introduced, which is a cryptographic proof. In mathematics, a surjection function simply means that for every element $ y $ in the codomain $ Y $ of function $ f $, there is at least one element $ x $ in the domain $ X $ of function $ f $ such that $ f(x) = y$.

An ASP scheme provides a proof $ \pi ​$ for a set of input asset commitments $ [ H_i ] ^n_{i=1} ​$, an output commitment $ H = H_{\hat i} + rG ​$ for $ \hat i = 1 \mspace{3mu} , \mspace{3mu} . . . \mspace{3mu} , \mspace{3mu} n ​$ and blinding factor $ r ​$. It proves that every output asset type is the same as some input asset type, while blinding which outputs correspond to which inputs. Such a proof $ \pi ​$ is secure if it is a zero-knowledge proof of knowledge for the blinding factor $ r ​$. Let $ H_{0_{A1}} ​$ and $ H_{0_{A2}} ​$ be blinded asset tags that commit to the same asset tag $ H_A ​$:

\[H_{0_{A1}} = H_A + r_1G \mspace{15mu} \mathrm{and} \mspace{15mu} H_{0_{A2}} = H_A + r_2G \tag{9}\]

Then

\[H_{0_{A1}} - H_{0_{A2}} = (H_A + r_1G) - (H_A + r_2G) = (r_1 - r_2)G \tag{10}\]

will be a signature key with secret key $ r_1 - r_2 $. Thus for an $ n $ distinct multiple asset type transaction, differences can be calculated between each output and all inputs, e.g. $ (out_A - in_A) , (out_A - in_B) \mspace{3mu} , \mspace{3mu} . . . \mspace{3mu} , \mspace{3mu} (out_A - in_n) $, and so on for all outputs. This has the form of a ring signature, and if $ out_A $ has the same asset tag as one of the inputs, the transaction signer will know the secret key corresponding to one of these differences, and be able to produce the ring signature. The ASP is based on the Back-Maxwell range proof (refer to Definition 9 of [1]), which uses a variation of Borromean ring signatures [18]. The Borromean ring signature, in turn, is a variant of the Abe-Ohkubo-Suzuki (AOS) ring signature [19]. An AOS ASP computes a ring signature that is equal to the proof $ \pi $ as follows:

• Calculate $ n $ differences $ H - H_{\hat i } $ for $ \hat i = 1 \mspace{3mu} , \mspace{3mu} . . . \mspace{3mu} , \mspace{3mu} n $, one of which will be equal to the blinding factor $ r $.
• Calculate a ring signature $ S $ of an empty message using the $ n $ differences.

The resulting ring signature $ S $ is equal to the proof $ \pi $, and the ASP consists of this ring signature $ S ​$ ([1], [14]).

Confidential Asset Scheme

Using the building blocks discussed in Basis of Confidential Assets, asset issuance, asset transactions and asset re-issuance can be performed in a confidential manner.

Asset Transactions

Confidential assets propose a scheme where multiple non-interchangeable asset types can be supported within a single transaction. This all happens within one blockchain and can theoretically improve the value of the blockchain by offering a service to more users. It can also enable extended functionality such as base layer atomic asset trades. The latter implies Alice can offer Bob $ 100 $ of asset type $ A $ for $ 50 $ of asset type $ B ​$ in a single transaction, both participants using a single wallet. In this case, no relationship between output asset types can be established or inferred, because all asset tags are blinded. Privacy can be increased, as the blinded asset types bring another dimension that needs to be unraveled in order to obtain user identity and transaction data by not having multiple single-asset transactions. Such a confidential asset scheme simplifies verification and complexity, and reduces on-chain data. It also prohibits censorship of transactions involving specific asset types, and blinds assets with low transaction volume where users could be identified very easily [1].

Assets originate in asset-issuance inputs, which take the place of coinbase transactions in confidential transactions. The asset type to pay fees must be revealed in each transaction, but in practice, all fees could be paid in only one asset type, thus preserving privacy. Payment authorization is achieved by means of the input signatures. A confidential asset transaction consists of the following data:

• A list of inputs, each of which can have one of the following forms:
  • a reference to an output of another transaction, with a signature using that output’s verification key; or
  • an asset issuance input, which has an explicit amount and asset tag.
• A list of outputs that contains:
  • a signature verification key;
  • an asset commitment $ H_0 $ with an ASP from all input asset commitments to $ H_0 $;
  • Pedersen commitment to an amount using generator $ H_0 $ in place of $ H $, with the associated Back-Maxwell range proof.
• A fee, listed explicitly as $ { (f_i , H_i) }_{i=1}^n $, where $ f_i $ is a non-negative scalar amount denominated in the asset with tag $ H_i $.

Every output has a range proof and ASP associated with it, which are proofs of knowledge of the Pedersen commitment opening information and asset commitment blinding factor. Every range proof can be considered as being with respect to the underlying asset tag $ H_A ​$, rather than the asset commitment $ H_0 ​$. The confidential transaction is restricted to only inputs and outputs with asset tag $ H_A ​$, except that output commitments minus input commitments minus fee sum to a commitment to $ 0 ​$ instead of to the point $ 0 ​$ itself [1].

However, confidential assets come at an additional data cost. For a transaction with $ m $ outputs and $ n $ inputs, in relation to the units of space used for confidential transactions, the asset commitment has size $ 1$, the ASP has size $ n + 1 $ and the entire transaction therefore has size $ m(n + 2) $ [1].

Asset Issuance

It is important to ensure that any auxiliary input $ A $ used to create asset tag $ H_A \in \mathbb G $ only be used once to prevent inflation by means of many independent issuances. Associating a maximum of one issuance with the spending of a specific UTXO can ensure this uniqueness property. Poelstra et al. [5] suggest the use of a Ricardian contract [11] to be hashed together with the reference to the UTXO being spent. This hash can then be used to generate the auxiliary input $ A $ as follows. Let $I $ be the input being spent (an unambiguous reference to a specific UTXO used to create the asset), let $ \widehat {RC} $ be the issuer-specified Ricardian contract, then the asset entropy $ E $ is defined as

\[E = \mathrm {Hash} ( \mathrm {Hash} (I) \parallel \mathrm {Hash} (\widehat {RC})) \tag{11}\]

The auxiliary input $ A $ is then defined as

\[A = \mathrm {Hash} ( E \parallel 0) \tag{12}\]

Note that a Ricardian contract $ \widehat {RC} $ is not crucial for entropy $ E $ generation, as some other unique NUMS value could have been used in its stead, but only suggested. Ricardian contracts warrant a bit more explanation and are discussed in Appendix B.

Every non-coinbase transaction input can have up to one new asset issuance associated with it. An asset issuance (or asset definition) transaction input then consists of the UTXO being spent, the Ricardian contract, either an initial issuance explicit value or a Pedersen commitment, a range proof and a Boolean field indicating whether reissuance is allowed ([1], [13]).

Asset Reissuance

The confidential asset scheme allows the asset owner to later increase or decrease the amount of the asset in circulation, given that an asset reissuance token is generated together with the initial asset issuance. Given an asset entropy $ E $, the asset reissuance capability is the element (asset tag) $ H_{\hat A} \in \mathbb G $ obtained using an alternative auxiliary input $ \hat A $ defined as

\[\hat A = \mathrm {Hash} ( E \parallel 1) \tag{13}\]

The resulting asset tag $ H_{\hat A} \in \mathbb G $ is linked to its reissuance capability, and the asset owner can assert their reissuance right by revealing the blinding factor $ r $ for the reissuance capability along with the original asset entropy $ E $. An asset reissuance (or asset definition) transaction input then consists of the spend of a UTXO containing an asset reissuance capability, the original asset entropy, the blinding factor for the asset commitment of the UTXO being spent, either an explicit reissuance amount or Pedersen commitment and a range proof [1].

The same mechanism can be used to manage capabilities for other restricted operations, e.g. to decrease issuance, to destroy the asset, or to make the commitment generator the hash of a script that validates the spending transaction. It is also possible to change the name of the default asset that is created upon blockchain initialization and the default asset used to pay fees on the network ([1], [13]).

Flexibility

ASPs prove that the asset commitments associated with outputs commit to legitimately issued asset tags. This feature allows compatible blockchains to support indefinitely many asset types, which may be added after the chain has been defined. There is room to adapt this scheme for optimal trade-off between ASP data size and privacy by introducing a global dynamic list of assets, whereby each transaction selects a subset of asset tags for the corresponding ASPs [1].

If all the asset tags are defined at the instantiation of the blockchain, this will be compatible with the Mimblewimble protocol. The range proofs used for the development of this scheme were based on the Back-Maxwell range proof scheme (refer to Definition 9 of [1]). Poelstra et al. [1] suggest more efficient range proofs, ASPs and use of aggregate range proofs. It is thus an open question whether Bulletproofs could fulfill this requirement.

Confidential Asset Implementations

Three independent implementations of confidential assets are summarized here. The first two implementations closely resemble the theoretical description given in [1], with the last implementation adding Bulletproofs’ functionality to confidential assets.

Elements Project

Elements [31] is an open source, sidechain-capable blockchain platform, providing access to advanced features such as Confidential Transactions and Issued Assets in Github: ElementsProject/elements [16]. It allows digitizable collectables, reward points and attested assets (e.g. gold coins) to be realized on a blockchain. The main idea behind Elements is to serve as a research platform and testbed for changes to the Bitcoin protocol. The Elements project’s implementation of confidential assets is called Issued Assets ([13], [14], [15]) and is based on its formal publication in [1].

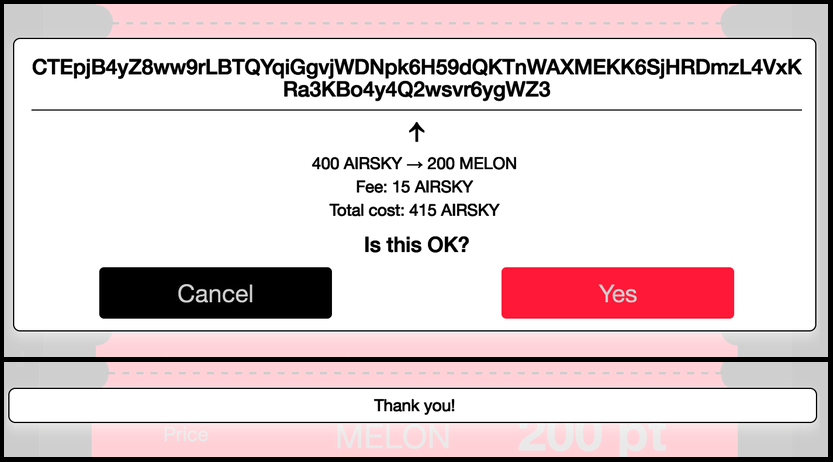
The Elements project hosts a working demonstration (shown in Figure 2) of confidential asset transfers involving five parties in Github: ElementsProject/confidential-assets-demo [17]. The demonstration depicts a scenario where a coffee shop owner, Dave, charges a customer, Alice, for coffee in an asset called MELON. Alice does not hold enough MELON and needs to convert some AIRSKY into MELON, making use of an exchange operated by Charlie. The coffee shop owner, Dave, has a competitor, Bob, who is trying to gather information about Dave’s sales. Due to the blockchain’s confidential transactions and assets features, he will not be able to see anything useful by processing transactions on the blockchain. Fred is a miner and does not care about the detail of the transactions, but he makes blocks on the blockchain when transactions enter his miner mempool. The demonstration also includes generating the different types of assets.

Figure 2: Elements Confidential Assets Transfer Demonstration [17]

Chain Core Confidential Assets

Chain Core [20] is a shared, multi-asset, cryptographic ledger, designed for enterprise financial infrastructure. It supports the coexistence and interoperability of multiple types of assets on the same network in their Confidential Assets framework. Chain Core is based on [1], and available as an open source project in Github: chain/chain [21], which has been archived. It has been succeeded by Sequence, a ledger-as-a-service project, which enables secure tracking and transfer of balances in a token format ([22], [23]). Sequence offers a free plan for up to 1,000,000 transactions per month.

Chain Core implements all native features as defined in [1]. It was also working towards implementing ElGamal commitments into Chain Core to make its Confidential Assets framework quantum secure, but it is unclear if this effort was concluded at the time the project was archived ([24], [25]).

Cloak

Chain/Interstellar [26] introduced Cloak [29], a redesign of Chain Core’s Confidential Assets framework to make use of Bulletproof range proofs [27]. It is available as an open source project in Github: interstellar/spacesuit [28]. Cloak is all about confidential asset transactions, called cloaked transactions, which exchange values of different asset types, called flavors. The protocol ensures that values are not transmuted to any other asset types, that quantities do not overflow, and that both quantities and asset types are kept secret.

A traditional Bulletproofs implementation converts an arithmetic circuit into a Rank-1 Constraint System (R1CS); Cloak bypasses arithmetic circuits and provides an Application Programmers Interface (API) for building a constraint system directly. The R1CS API consists of a hierarchy of task-specific “gadgets”, and is used by the Prover and Verifier alike to allocate variables and define constraints. Cloak uses a collection of gadgets such as “shuffle”, “merge”, “split” and “range proof” to build a constraint system for cloaked transactions. All transactions of the same size are indistinguishable, because the layout of all the gadgets is only determined by the number of inputs and outputs.

At the time of writing this report, the Cloak development was still ongoing.

Conclusions, Observations and Recommendations

• The idea to embed a Ricardian contract in the asset tag creation as suggested by Poelstra et al. [1] warrants more investigation for a new confidential blockchain protocol such as Tari. Ricardian contracts could be used in asset generation in the probable second layer.

• Asset commitments and ASPs are important cryptographic primitives for confidential asset transactions.

• The Elements project implemented a range of useful confidential asset framework features and should be critically assessed for usability in a probable Tari second layer.

• Cloak has the potential to take confidential assets implementation to the next level in efficiency and should be closely monitored. Interstellar is in the process of fully implementing and extending Bulletproofs for use in confidential assets.

• If confidential assets are to be implemented in a Mimblewimble blockchain, all asset tags must be defined at their instantiation, otherwise they will not be compatible.

References

[1] A. Poelstra, A. Back, M. Friedenbach, G. Maxwell and P, Wuille, “Confidential Assets”, Blockstream [online]. Available: https://blockstream.com/bitcoin17-final41.pdf. Date accessed: 2018‑12‑25.

“Confidential Assets, A. Poelstra et al., Blockstream”

[2] Wikipedia: “Discrete Logarithm” [online]. Available: https://en.wikipedia.org/wiki/Discrete_logarithm. Date accessed: 2018‑12‑20.

[3] A. Sadeghi and M. Steiner, “Assumptions Related to Discrete Logarithms: Why Subtleties Make a Real Difference” [online]. Available: http://www.semper.org/sirene/publ/SaSt_01.dh-et-al.long.pdf. Date accessed: 2018‑12‑24.

“Assumptions Related to Discrete Logarithms: Why Subtleties Make a Real Difference, A. Sadeghi et al.”

[4] G. Maxwell, “Confidential Transactions Write up” [online]. Available: https://people.xiph.org/~greg/confidential_values.txt. Date accessed: 2018‑12‑10.

“Confidential Transactions Write up, G. Maxwell”

[5] A. Gibson, “An Investigation into Confidential Transactions”, July 2018 [online]. Available: https://github.com/AdamISZ/ConfidentialTransactionsDoc/blob/master/essayonCT.pdf. Date accessed: 2018‑12‑22.

“An Investigation into Confidential Transactions, A. Gibson, July 2018”

[6] Pedersen-commitment: An Implementation of Pedersen Commitment Schemes [online]. Available: https://hackage.haskell.org/package/pedersen-commitment. Date accessed: 2018‑12‑25.

“Pedersen-commitment: An Implementation of Pedersen Commitment Schemes”

[7] B. Franca, “Homomorphic Mini-blockchain Scheme”, April 2015 [online]. Available: http://cryptonite.info/files/HMBC.pdf. Date accessed: 2018‑12‑22.

“Homomorphic Mini-blockchain Scheme, B. Franca, April 2015”

[8] C. Franck and J. Großschädl, “Efficient Implementation of Pedersen Commitments Using Twisted Edwards Curves”, University of Luxembourg [online]. Available: http://orbilu.uni.lu/bitstream/10993/33705/1/MSPN2017.pdf. Date accessed: 2018‑12‑22.

“Efficient Implementation of Pedersen Commitments Using Twisted Edwards Curves, C. Franck and J. Großschädl, University of Luxembourg”

[9] A. Poelstra, “Mimblewimble”, October 2016 [online]. Available: http://diyhpl.us/~bryan/papers2/bitcoin/mimblewimble-andytoshi-draft-2016-10-20.pdf. Date accessed: 2018‑12‑13.

“Mimblewimble, A. Poelstra, October 2016”

[10] A. Poelstra, “Mimblewimble Explained”, November 2016 [online]. Available: https://www.weusecoins.com/mimble-wimble-andrew-poelstra/. Date accessed: 2018‑12‑10.

“Mimblewimble Explained, A. Poelstra, November 2016”

[11] I. Grigg, “The Ricardian Contract”, First IEEE International Workshop on Electronic Contracting. IEEE (2004) [online]. Available: http://iang.org/papers/ricardian_contract.html. Date accessed: 2018‑12‑13.

“The Ricardian Contract, First IEEE International Workshop on Electronic Contracting. IEEE (2004), I. Grigg”

[12] D. Koteshov, “Smart vs. Ricardian Contracts: What’s the Difference?” February 2018 [online]. Available: https://www.elinext.com/industries/financial/trends/smart-vs-ricardian-contracts/. Date accessed: 2018‑12‑13.

“Smart vs. Ricardian Contracts: What’s the Difference?, D. Koteshov, February 2018”

[13] Elements by Blockstream: “Issued Assets - You can Issue your own Confidential Assets on Elements”
[online]. Available: https://elementsproject.org/features/issued-assets. Date accessed: 2018‑12‑14.

“Issued Assets - You can Issue your own Confidential Assets on Elements, Elements by Blockstream”

[14] Elements by Blockstream: “Issued Assets - Investigation, Principal Investigator: Andrew Poelstra” [online]. Available: https://elementsproject.org/features/issued-assets/investigation. Date accessed: 2018‑12‑14.

“Issued Assets - Investigation, Principal Investigator: Andrew Poelstra, Elements by Blockstream”

[15] Elements by Blockstream: “Elements Code Tutorial - Issuing your own Assets” [online]. Available: https://elementsproject.org/elements-code-tutorial/issuing-assets. Date accessed: 2018‑12‑14.

“Elements Code Tutorial - Issuing your own Assets, Elements by Blockstream”

[16] Github: ElementsProject/elements [online]. Available: https://github.com/ElementsProject/elements. Date accessed: 2018‑12‑18.

[17] Github: ElementsProject/confidential-assets-demo [online]. Available: https://github.com/ElementsProject/confidential-assets-demo. Date accessed: 2018‑12‑18.

[18] G. Maxwell and A. Poelstra, “Borromean Ring Signatures” (2015) [online]. Available: http://diyhpl.us/~bryan/papers2/bitcoin/Borromean%20ring%20signatures.pdf. Date accessed: 2018‑12‑18.

“Borromean Ring Signatures (2015), G. Maxwell and A. Poelstra”

[19] M. Abe, M. Ohkubo and K. Suzuki, “1-out-of-n Signatures from a Variety of Keys” [online]. Available: https://www.iacr.org/cryptodb/archive/2002/ASIACRYPT/50/50.pdf. Date accessed: 2018‑12‑18.

“1-out-of-n Signatures from a Variety of Keys, M. Abe, M. Ohkubo and K. Suzuki”

[20] Chain Core [online]. Available: https://chain.com/docs/1.2/core/get-started/introduction. Date accessed: 2018‑12‑18.

[21] Github: chain/chain [online]. Available: https://github.com/chain/chain. Date accessed: 2018‑12‑18.

[22] Chain: “Sequence” [online]. Available: https://chain.com/sequence. Date accessed: 2018‑12‑18.

[23] Sequence Documentation [online]. Available: https://dashboard.seq.com/docs. Date accessed: 2018‑12‑18.

[24] O Andreev: “Hidden in Plain Sight: Transacting Privately on a Blockchain - Introducing Confidential Assets in the Chain Protocol”, Chain [online]. Available: https://blog.chain.com/hidden-in-plain-sight-transacting-privately-on-a-blockchain-835ab75c01cb. Date accessed: 2018‑12‑18.

“Hidden in Plain Sight: Transacting Privately on a Blockchain - Introducing Confidential Assets in the Chain Protocol O. Andreev”

[25] Blockchains in a Quantum Future - Protecting Against Post-Quantum Attacks on Cryptography [online]. Available: https://blog.chain.com/preparing-for-a-quantum-future-45535b316314. Date accessed: 2018‑12‑18.

“Blockchains in a Quantum Future - Protecting Against Post-Quantum Attacks on Cryptography”

[26] Inter/stellar website [online]. Available: https://interstellar.com. Date accessed: 2018‑12‑22.

[27] C. Yun, “Programmable Constraint Systems for Bulletproofs” [online]. Available: https://medium.com/interstellar/programmable-constraint-systems-for-bulletproofs-365b9feb92f7. Date accessed: 2018‑12‑22.

“Programmable Constraint Systems for Bulletproofs, Interstellar, C. Yun”

[28] Github: interstellar/spacesuit [online]. Available: https://github.com/interstellar/spacesuit/blob/master/spec.md. Date accessed: 2018‑12‑18.

[29] Github: interstellar/spacesuit/spec.md [online]. Available: https://github.com/interstellar/spacesuit/blob/master/spec.md. Date accessed: 2018‑12‑18.

[30] Wikipedia: “Ricardian Contract” [online]. Available: https://en.wikipedia.org/wiki/Ricardian_contract. Date accessed: 2018‑12‑21.

[31] Wikipedia: “Elements by Blockstream” [online]. Available: https://elementsproject.org. Date accessed: 2018‑12‑21.

Appendices

Appendix A: Definition of Terms

Definitions of terms presented here are high level and general in nature. Full mathematical definitions are available in the cited references.

• Discrete Logarithm/Discrete Logarithm Problem (DLP): In the mathematics of real numbers, the logarithm $ \log_b^a $ is a number $ x $ such that $ b^x=a $, for given numbers $ a $ and $ b $. Analogously, in any group $ G $, powers $ b^k $ can be defined for all integers $ k $, and the discrete logarithm $ \log_ba $ is an integer $ k $ such that $ b^k=a $. Algorithms in public-key cryptography base their security on the assumption that the discrete logarithm problem over carefully chosen cyclic finite groups and cyclic subgroups of elliptic curves over finite fields has no efficient solution ([2], [3]).

“In the mathematics of real numbers, the logarithm log_b(a) is a number x such that …”

Appendix B: Ricardian Contracts vs. Smart Contracts

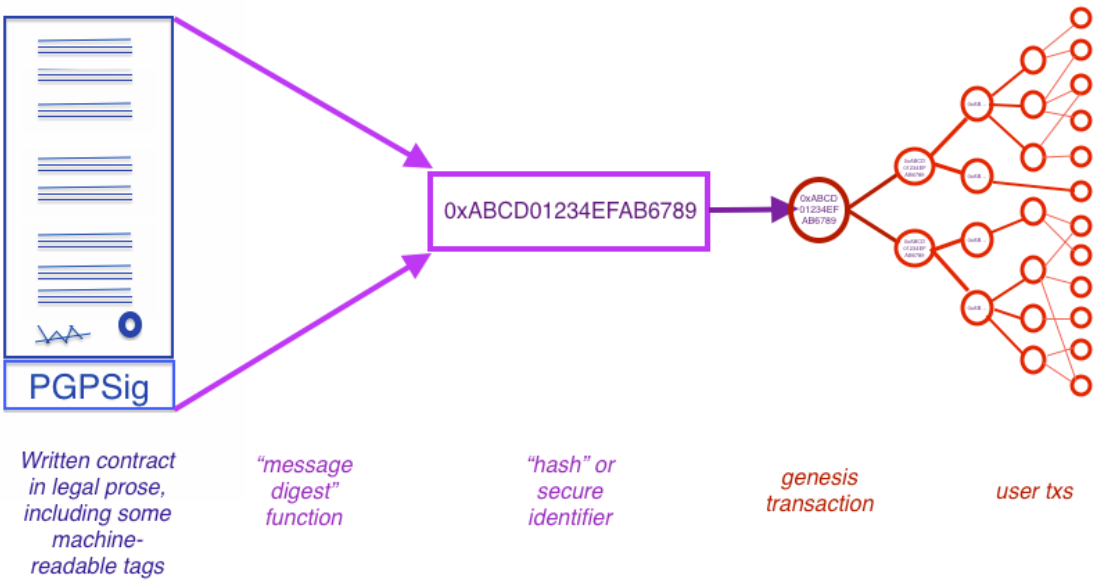
A Ricardian contract is “a digital contract that defines the terms and conditions of an interaction, between two or more peers, that is cryptographically signed and verified, being both human and machine readable and digitally signed” [12]. With a Ricardian contract, the information from the legal document is placed in a format that can be read and executed by software. The cryptographic identification offers high levels of security. The main properties of a Ricardian contract are (also refer to Figure 1):

• human readable;
• document is printable;
• program parsable;
• all forms (displayed, printed and parsed) are manifestly equivalent;
• signed by issuer;
• can be identified securely, where security means that any attempts to change the linkage between a reference and the contract are impractical.

Figure 1: Bowtie Diagram of a Ricardian Contract [12]

Ricardian contracts are robust (due to identification by cryptographic hash functions), transparent (due to readable text for legal prose) and efficient (due to computer markup language to extract essential information [30].

A smart contract is “a computerized transaction protocol that executes the terms of a contract. The general objectives are to satisfy common contractual conditions” [12]. With smart contracts, digital assets can be exchanged in a transparent and non-conflicting way. They provide trust. The main properties of a smart contract are:

• self-executing (it doesn’t run unless someone initiates it);
• immutable;
• self-verifying;
• auto-enforcing;
• cost saving;
• removes third parties or escrow agents.

It is possible to implement a Ricardian contract as a smart contract, but not in all instances. A smart contract is a pre-agreed digital agreement that can be executed automatically. A Ricardian contract records “intentions” and “actions” of a particular contract, no matter if it has been executed or not. Hashes of Ricardian contracts can refer to documents or executable code ([12], [30]).

The Ricardian contract design pattern has been implemented in several projects and is free of any intellectual property restrictions [30].

Contributors

• https://github.com/hansieodendaal
• https://github.com/philipr-za
• https://github.com/neonknight64
• https://github.com/anselld